SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
1. 문제설명
N*N 크기의 정사각형 모양의 방에 사람들이 앉아 있다.
점심을 먹기 위해 아래 층으로 내려가야 하는데, 밥을 빨리 먹기 위해 최대한 빠른 시간 내에 내려가야 한다.
방 안의 사람들은 P로, 계단 입구를 S라고 했을 때 [Fig. 1]은 사람의 위치와 계단 입구의 위치를 표시한 모습이다.
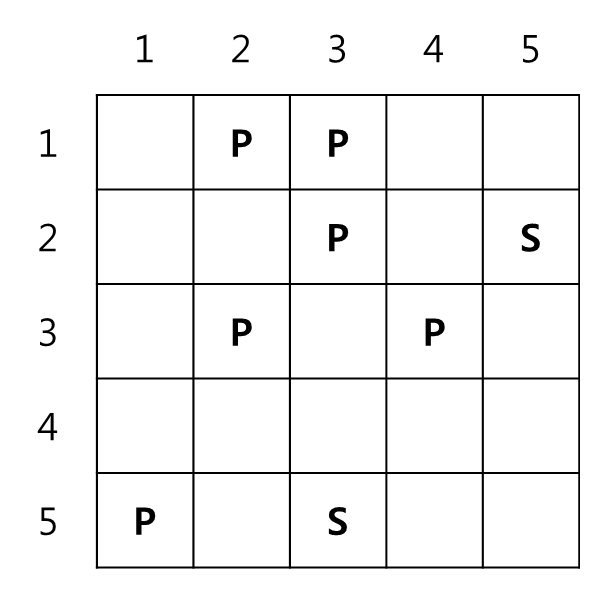
[Fig. 1]
이동 완료 시간은 모든 사람들이 계단을 내려가 아래 층으로 이동을 완료한 시간이다.
사람들이 아래층으로 이동하는 시간은 계단 입구까지 이동 시간과 계단을 내려가는 시간이 포함된다.
① 계단 입구까지 이동 시간
- 사람이 현재 위치에서 계단의 입구까지 이동하는데 걸리는 시간으로 다음과 같이 계산한다.
- 이동 시간(분) = | PR - SR | + | PC - SC |
(PR, PC : 사람 P의 세로위치, 가로위치, SR, SC : 계단 입구 S의 세로위치, 가로위치)
② 계단을 내려가는 시간
- 계단을 내려가는 시간은 계단 입구에 도착한 후부터 계단을 완전히 내려갈 때까지의 시간이다.
- 계단 입구에 도착하면, 1분 후 아래칸으로 내려 갈 수 있다.
- 계단 위에는 동시에 최대 3명까지만 올라가 있을 수 있다.
- 이미 계단을 3명이 내려가고 있는 경우, 그 중 한 명이 계단을 완전히 내려갈 때까지 계단 입구에서 대기해야 한다.
- 계단마다 길이 K가 주어지며, 계단에 올라간 후 완전히 내려가는데 K 분이 걸린다.
사람의 위치와 계단 입구의 위치 및 계단의 길이 정보가 표시된 N*N 크기의 지도가 주어진다.
이때, 모든 사람들이 계단을 내려가 이동이 완료되는 시간이 최소가 되는 경우를 찾고,
그 때의 소요시간을 출력하는 프로그램을 작성하라.
[예시]
방의 한 변의 길이 N 이 5인 지도가 [Fig. 2]와 같이 주어진 경우를 생각해보자.
지도 내에 1 은 사람을 나타내고, 2 이상 10 이하의 숫자는 계단의 입구를 나타내며 해당 숫자는 계단의 길이를 의미한다.
[Fig. 2]에는 사람 6명이 있고, 계단은 2개가 있으며 길이는 각각 3과 5이다.
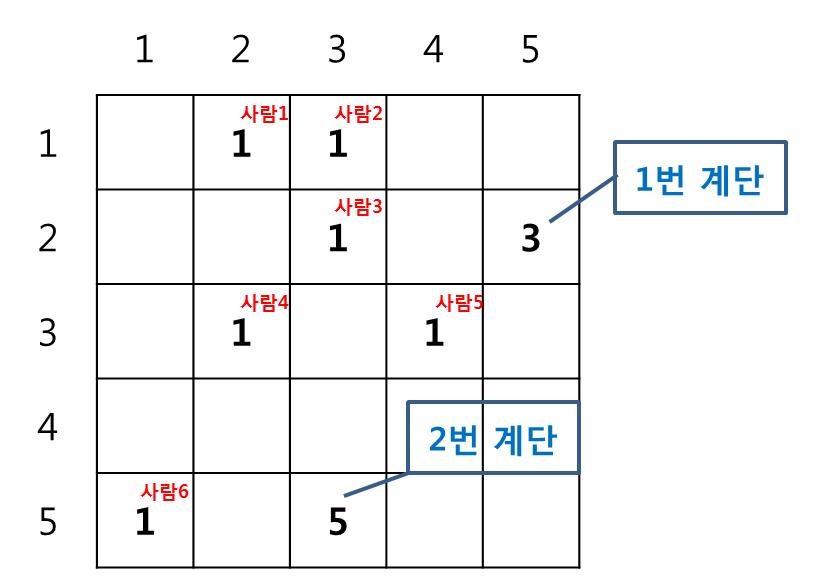
다음은 이동 완료되는 시간이 최소가 되는 경우 중 하나이다.
- 1번, 2번, 3번 사람은 길이가 3인 1번 계단을 통해 이동
- 4번, 5번, 6번 사람은 길이가 5인 2번 계단을 통해 이동

이 경우, 모든 사람이 계단을 내려가 이동 완료하는 최소 시간은 9분이다.
다른 예시로, 한 변의 길이가 N인 방에 [Fig. 3]과 같이 배치되어 있는 경우를 생각해보자.
지도 내에 1 은 사람을 나타내고, 2 이상 10 이하의 숫자는 계단의 입구를 나타내며 해당 숫자는 계단의 길이를 의미한다.
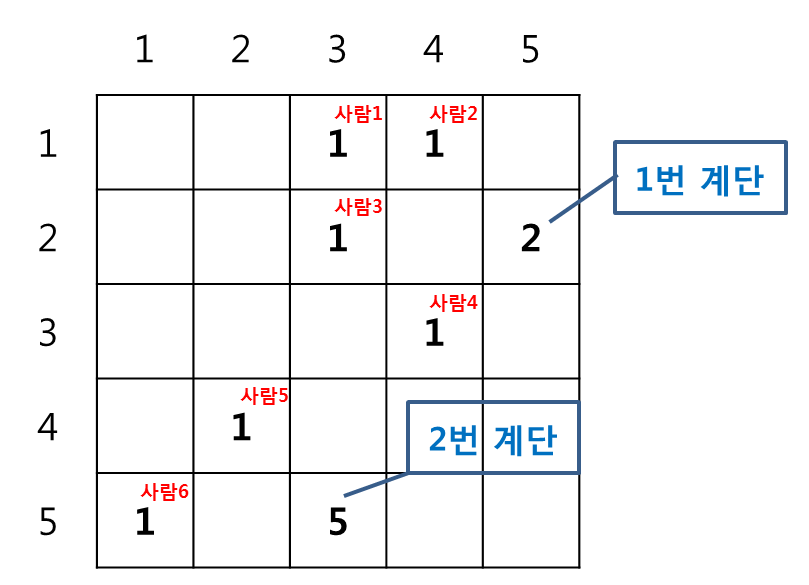
다음은 이동이 완료되는 시간이 최소가 되는 경우 중 하나이다.
- 1번, 2번, 3번, 4번 사람은 길이가 2인 1번 계단을 통해 이동
- 5번, 6번 사람은 길이가 5인 2번 계단을 통해 이동

이 경우, 모든 사람이 계단을 내려가 이동 완료하는 최소 시간은 8분이다.
[제약 사항]
1. 시간제한 : 최대 50개 테스트 케이스를 모두 통과하는데, C/C++/Java 모두 3초
2. 방의 한 변의 길이 N은 4 이상 10 이하의 정수이다. (4 ≤ N ≤ 10)
3. 사람의 수는 1 이상 10 이하의 정수이다. (1 ≤ 사람의 수 ≤ 10)
4. 계단의 입구는 반드시 2개이며, 서로 위치가 겹치지 않는다.
5. 계단의 길이는 2 이상 10 이하의 정수이다. (2 ≤ 계단의 길이 ≤ 10)
6. 초기에 입력으로 주어지는 사람의 위치와 계단 입구의 위치는 서로 겹치지 않는다.
[입력]
입력의 맨 첫 줄에는 총 테스트 케이스의 개수 T가 주어지고, 그 다음 줄부터 T개의 테스트 케이스가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 방의 한 변의 길이 N이 주어진다.
다음 N줄에는 N*N 크기의 지도의 정보가 주어진다.
지도에서 1은 사람을, 2 이상은 계단의 입구를 나타내며 그 값은 계단의 길이를 의미한다.
[출력]
테스트 케이스의 개수만큼 T줄에 T개의 테스트 케이스 각각에 대한 답을 출력한다.
각 줄은 "#x"로 시작하고 공백을 하나 둔 다음 정답을 출력한다. (x는 1부터 시작하는 테스트 케이스의 번호이다)
정답은 이동이 완료되는 최소의 시간을 출력한다.
| 입력 10 5 0 1 1 0 0 0 0 1 0 3 0 1 0 1 0 0 0 0 0 0 1 0 5 0 0 5 0 0 1 1 0 0 0 1 0 2 0 0 0 1 0 0 1 0 0 0 1 0 5 0 0 … |
출력
#1 9
#2 8 ... |
2. 문제 풀이
1. dp로 푸는 풀이가 있다고 하는데 dp는 아에 생각이 나지 않아 풀이법을 검색해서 풀었다. 아이디어는 순열로 두개의 계단 중에서 1번 계단으로 가는 사람과 2번 계단으로 가는 사람을 다 해봐서 완전 탐색으로 푸는 것이였다.
2. 사람의 위치와 계단의 위치를 각각 저장해 두고
3. 사람을 조합으로 두그룹으로 나눠 첫번째 그룹과 첫번째 계단 두번째 그룹과 두번째 계단을 각각 dfs 함수에 넣어 더 큰 시간을 해당 경우의 수의 시간으로 저장한다.
4. dfs 함수는 그룹과 계단의 위치를 매개변수로 받고 s에는 각 사람들이 계단에 도착하는 시간을 저장, e에는 계단을 내려가기 시작한 사람들이 이동을 완료하는 시간을 저장, t 는 현재 시간이고, c는 현재 계단을 이용하는 사람의 수이다.
5. s에 값이 있다면 아직 이동해야할 사람이 있다는 뜻이므로 while문을 실행한다. 현재 시간에 이동을 완료한 사람이 있다면, e에서 pop해주고 c를 1 빼준다. 현재 시간에 이동을 시작한 사람이 있다면, e에서 pop해주고 c을 1빼준다. 현재 시간에 이동을 시작한 사람이 있다면, s에서 pop해주고 e에 이동 완료 시간을 push하고 c을 1 더해준다.
(도착하고 1분후에 이동을 시작하기 때문에 s[0] <= t 가 아닌 s[0] < t 로 했다.)
6. s가 비게 되면 t에 방금 이동을 시작한 사람이 이동을 완료하는 시간을 저장하고 while 문을 끝낸다.
7. 위의 과정으로 모든 경우의 수를 확인한 후, 가장 적은 시간을 total에 계속 갱신하여 출력한다.
from itertools import combinations
from collections import deque
def dfs(people, stair):
s = []
# 계단까지 가는 시간
for person in people:
s.append(abs(person[0] - stair[0]) + abs(person[1] - stair[1]))
# 계단을 내려가서 도착하는 시간
s = deque(sorted(s))
e = deque()
t = 0
c = 0
while s:
t += 1
while e and e[0] == t:
e.popleft()
c -= 1
while s[0] < t:
if c < 3:
s.popleft()
if not s:
t += board[stair[0]][stair[1]]
break
e.append(t + board[stair[0]][stair[1]])
c += 1
else:
break
return t
T = int(input())
for test_case in range(1, T+1):
N = int(input())
board = [list(map(int, input().split())) for _ in range(N)]
people = []
stair = []
for i in range(N):
for j in range(N):
if board[i][j] == 1:
people.append((i, j))
elif board[i][j] > 1:
stair.append((i, j))
total = 1e9
for n in range(N):
for people1 in combinations(people, n):
people2 = list(set(people) - set(people1))
t = max(dfs(people1, stair[0]), dfs(people2, stair[1]))
total = min(total, t)
print(f'#{test_case}', total)'Programming > python' 카테고리의 다른 글
| 백준 15684 : 사다리 조작 [파이썬] (0) | 2023.03.20 |
|---|---|
| 백준 12100 : 2048(Easy) [파이썬] (0) | 2023.03.13 |
| SWEA 원자 소멸 시뮬레이션 [파이썬] (0) | 2023.03.04 |
| 백준 6087 : 레이저 통신 [파이썬] (0) | 2023.02.25 |
| 백준 2206 : 벽 부수고 이동하기 [파이썬] (0) | 2023.02.25 |